it from bit ??
allow me to replace it, the bit, by 'spit' :-)
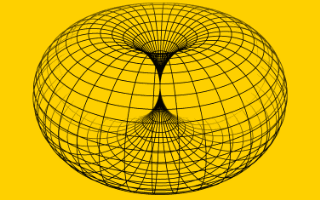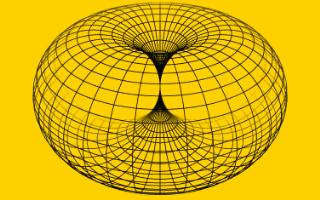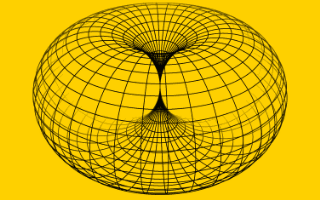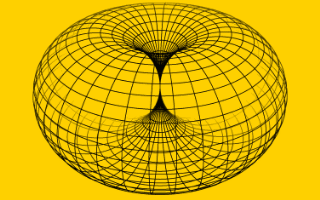
In the horn torus model of 'it' resp. 'all that' we have identified the standard dynamic horn torus as 'smallest' elementary unit, which turns with one rotation ('spin') per one revolution and vice versa. The image is reducible to pairs of bits: (1,1), (-1,1), (1,-1), (-1,-1). Zero (0), what would represent static of a unit, primarily does not occur, because horn tori are dynamic and never stand still. Static is not allowed. We take that pairs as complex numbers with integer parts. The real part represents spin, 1 for left (L), -1 for right (R), the imaginary part represents time, 1 for our world (i·t), -1 for anti-world (-i·t). The unit now is a spin-related binary digit, in short: spin-bit, or even, if you allow, shorter: spit. All that - our real world - is constructed from such complex units (L,i·t) and (R,i·t): it from spit.
Figuratively a horn torus rolls along its axis of rotation with the constant rate of revolution - in real with speed of light - and thereby increases its size to the unrolled 'distance' on the axis, maintaining the spin (rate and direction of rotation). A fixed point on the horn torus surface then describes an intricate 'unrolling line', trajectory or cycloid to the infinite. The line together with its completion to a size of the horn torus close to zero forms one unique 'fundamental entity'.
A 'spit' cannot be isolated and treated separately, as a bit can be. A 'spit' always is part of an entity that spreads all over the universe. All spatial points, infinite many, are connected to all other points, graphically illustrated by the array of all, infinite many, nested horn torus entities. They touch one another on the common main symmetry axis ('time') in every spatial point, and in all spatial points every entity is represented by a horn torus of a particular size, belonging to that individual point.
spin:
rotation of a horn torus
here without revolution
- not realized in nature,
spit (x,0) doesn't occur
(time always 'rolls' on!)
→
a bit more explanation
close animation