Horn Torus & Physics
'Geometry of Everything'
by Wolfgang W. Daeumler
The geometrical horn torus model is a proposal for a different approach to physical questions by the attempts to describe fundamental physical
processes graphically, namely in the form of
dynamically
interlaced horn tori. These are eminently suitable to illustrate complex numbers and their manifold properties, when the imaginary part is
represented by numbers connected to revolutions around the torus bulge (longitudes), the real part by numbers related to rotations around the main
symmetry axis (latitudes). The arising physical-geometrical analogies are amazing! Convince yourself:
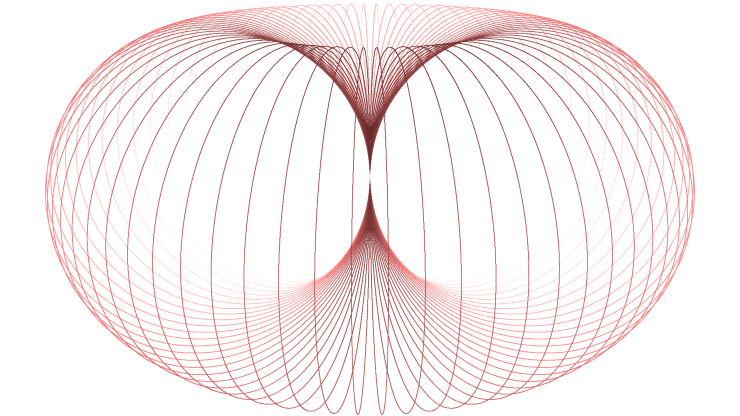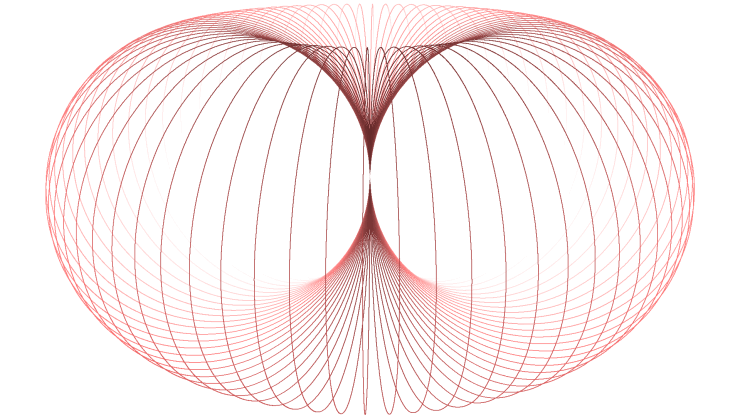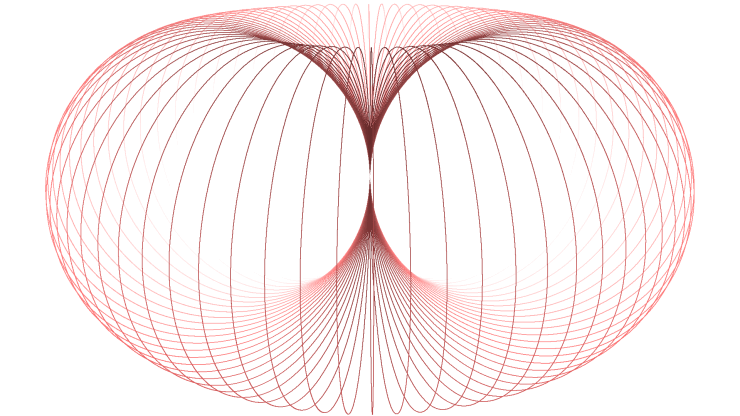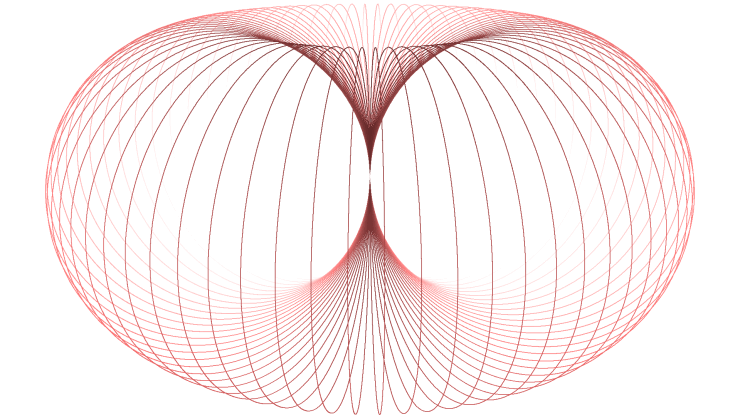
⟨ ⟩
The horn torus, that we are discussing here, shall not be seen as something like a solid figure, embedded in a three-dimensional world. Our horn
tori span a space of their own as dynamically uncoiling coordinates . They bear, as entities within this space, highest symmetry, incredible
complexity and creative capabilities. In the pure analogous model they symbolise manifold intrinsic properties of complex numbers, what
enables them to act as quite efficient visual aids for many aspects of physical processes and laws on a fundamental level (space, time, physical objects, 'particles',
interaction, ...), which often are not easily comprehensible by normal and even scientifically trained everyday's understanding, and for which
physicists unfortunately not have contributed any appropriate pictorial associations to match one's receptive mental imagery. Now interlaced
(nested) dynamic horn tori allow to build bridges between abstract mathematics and our inherent thinking. After intensive
familiarization with the model, its analogous images and its geometrically representable dynamics, many physical terms, concepts and phenomena
appear no longer mysterious and unexplained but
become inevitable, logical, clear and evident*. Nevertheless the horn torus model doesn't claim to be a consistent physical or mathematical theory.
Regard it as suggestion to leave fixed habits of conventional mainstream thinking - now and then, playfully, just for fun! Sometimes crackpot ideas
inspire. The matter is intended to be an exciting game, to exercise imaginative power, to improve abstract thinking and to generate lots of aha
moments. It has no esoteric connection! It's just based on mathematics, complex numbers and their arithmetic, associated geometry and a
unique code ... continue or enter step by step
This private website exists since 2006 (in German language since 2000 as DornTorus.de, some texts date back to 1988 -
author used to be a theoretical physicist), it is written in meanwhile partly obsolete HTML4 and not optimized for smartphones. It contains
countless explaining images and animations, that are best viewed on a bigger screen. Relevant information is spread over a great many reciprocally
linked pages, occasionally - sorry for that (it's part of the game) - a little bit hidden, often embellished with algorithmic art. Along with some
related websites, also part of our game, the presentation might be classified as an interdisciplinary art project with a little spice of
scientificity , at least with a deeper meaning:
DornTorus.de
horntorus.de
BTW: when searching online for 'horn torus' you often find sites about 'sacred geometry' and similar odd topics but hardly serious, reasonable and
scientifically relevant publications which exceed e.g. WolframMathWorld ... really weird !
2023:
There are now, four years later, many publications that contain the figure horn torus (see e.g.
Google Scholar). This page, however, remains
unchanged since 2019.
*) many physical phenomena, conditions and relations we do not really understand at all and quite often don't even question our as reality declared
perception of them: space and time, physical objects as contained structures, 'particles', their interactions, energy, mass, force, impulse,
location and 'movement in space', constancy of the speed of light, its value as maximum limit, constants, quantization of values, spin, isospin,
(color-)charge, non-locality, quantum entanglement, symmetries, invariances, Pauli principle, determinism, causality, complexity, arrow and reversal
of time, antimatter, singularities, infinity, cosmology ...
Rigorous mathematization of space, time and all physical objects, isolated from our perception (including three-dimensional space!), seems to be the
only method for reducing fundamental laws of nature to a very few principles, possibly to one unique code, that rules our universe.
The horn torus model - as an intellectual game - pursues this goal. Here an excerpt (a kind of concluding summary) from the texts:
|
..... Now, I think (or hope), we have done all conceptual and mental preparations to face most fundamental questions in our perception of what we
call physics: now we have to find and describe the cause for locomotion of particles or, more generally speaking, physical objects within the space
they populate, independent how space is defined. That cause we usually call force. We distinguish four different fundamental forces: gravity,
electromagnetism, strong and weak force. All are manifestations of any mysterious 'interaction' between particles resp. physical objects.
Physicists are able to describe them mathematically, calculate exact values, and make accurate predictions, but the deep principle or
mechanism behind that interaction still is completely unknown. I am convinced that linear vector spaces, basis of most physical theories, never will
lead to the final answer. Loop QG fans with their different definition of space have a distinctly better chance! And users of non-linear horn tori
already have an approach: The principle first (explanation below): a horn torus, unrolling along the trajectories of other horn tori which are located in the same spatial point, is forced to change its rotation speed, and therefore also changes its size, because within the same entity a firm correlation exists between size and rotation speed of every horn torus. At a certain distance from the 'origin' or also from the unit horn torus, there is always only one single definite ratio of the angular velocities, revolution to rotation, and size is known to be inversely proportional to the revolution angular velocity. The entire entity - together with its origin and with all associated particles - shifts to new positions related to other entities without changing its internal structure, and that means the particles move closer or move away from other particles, depending on the change in the rotational speed. For clarification, once again: every single entity has exactly the same dynamic properties, all entities - except their mirror image - show exactly the same shape and behaviour (after all they only are images of abstract complex numbers resp. manifolds, we know!). A horn torus of a certain size and revolution angular velocity always has its place at exactly one single position within the entity, with a fixed distance from the origin (or from the unit horn torus, or from other resonances, ...). A specific size of the horn torus always implicates a certain ratio of bulge revolution to rotation angular velocity. If the rotation changes, the size also changes, and that means that the distance (= size) from the origin, from the unit horn torus and from the particle cascade is different in the new spatial point. To illustrate an entity, we remember this animation. It shows - schematically shortened - the dynamic geometrical structure of one singled out entity, but only its short section between the ratios 1:4 and 4:1 (ratio of bulge revolution to rotation) and with constant rotation. Some members of the particle cascade are highlighted: the electron is represented by the ratio 1:2, the adjacent unit horn torus (for metrisation) appears as an unimpressive bent circle at 1:1. The most striking Lissajous figures are emphasized. Between them there is in addition an infinite number of windings and blades not shown in the figure. How does the change of rotation during bulge revolution occur? The unrolling line (trajectory) on the surface of a large horn torus consists of many closely spaced windings per one turn of the bulge, the larger the torus, the more windings, nearly parallel to the bulge latitudes. When any horn torus of another entity, sharing the same spatial point, has to follow this line, that undoubtedly has an influence on its own rotation (the unrolling should take place - figuratively - without 'slippage'). However, since this horn torus not only unrolls on one single different horn torus but on all existing in this spatial point simultaneously, a kind of 'mean value' surely will be established, according to values and directions of rotation (left or right, above mentioned mirror image). The image rapidly becomes very complicated, but endures as an explanation for the principle of interaction between entities (and associated particles) quite descriptive as a comprehensible tool. Quite automatically, unspectacularly plausible, and here almost not worth to be mentioned in more than a subordinate sentence, our horn torus model implies a unification of all four modes of interaction - a unification of all four fundamental forces! The principle always is the same: unrolling, adjusting the horn torus size to the changing rotation and finally simultaneously (more precisely: after a Planck time) shifting the entire entity including all contained particles. The principle in all cases is identical, only the portion on the entity where the described mechanism takes place is different: gravity acts in the region of the large horn tori with many windings and no significant resonances, electromagnetism starts from the electron (resonance 1:2) and proceeds in both directions, to the large horn tori as a free 'spreading' photon, and between electron and first nucleon (proton, 2:1) as a reciprocating 'caged' photon, the strong interaction is confined to the region between the resonances 2:1 and 3:1, while the weak interaction reaches up to the resonance 4:1. Forces in regions of the entity with higher ratio (smaller horn tori) are possible but not known as additional sort of force yet. Due to the higher ratio (revolution >> rotation) there likely are less rotation induced effects (weaker than weak force). The cause for locomotion of particles - in other words: force between particles - is now reduced to one single mechanism. Only the name for this unified force is different in distinct portions of an entity. Different values result from very different rotation speeds in the respective portions. Superpositions of Lissajous figures may matter additionally. So, there is a wide field for further thoughts left, always aware that with the horn torus model we only use an artificially established analogue representation of abstract mathematical manifolds. Only the latter, as basis, allow us to undertake universally valid calculations, which now may start: mathematical elaboration is required from now on ..... ..... and here we leave the mere imagination, describable in common speech. Here starts physics. In accustomed manner, using sophisticatedly invented formulations of naturally preexisting mathematical rules. - Unfortunately these rules seem to be too 'simple' to match complexities of human perception and thinking: rules within - for humans - simply imaginable and more or less conceivable spaces with their simple linear coordinates require a complex language for description. Obviously one has to pay this price for comprehension, or - my preference - play a game with reverse relations: travel in a space spanned by very complex coordinates and you only have to deal with very simple rules - fundamental mathematical rules. They exist from the beginning of our universe, and generations of mathematicians and physicists have learned to handle them perfectly. So, let's get started ..... ⇑ |
mathematicians may visit a short digression regarding an alternate for the Riemann sphere:
conformal mapping sphere ↔ horn torus , published in this article
horn torus mapping in general
The Big Hiss
 Wolfgang W. Däumler |