The reality, I intend to write about here, concerns a fundamental 'real world', in which no consciousness exists, that is able to reflect about
itself and about its connection to everything having any correlation or interaction with and an influence on it. The description of my intention
already turns out to be difficile - even these chosen words contain semantic meanings, which don't occur in a 'real world'. Yes, I know, full
abstraction from human speech is impossible to attain and even difficult to approach by strict mathematicians, no matter which high level of
fundamental formalism they claim to pursue. Nevertheless, any weird conjunction of colloquial speech and mathematical methods seems to be the only
means for us humans to treat and express rules of reality, which clearly do not match our consciousness, thought structure and faculty of
imagination.
Such an 'unconscious' reality is not knowable, and - sorry! - all philosophers who claim to possess a valid definition for an absolute, 'really real'
reality, are wrong, because every definition contains terms that only are invented by a consciousness and do not exist without. So, I'm not
even going to add another useless version, but will try to name such terms with a view to eliminate them from my vision and to approximate a kind of
mathematically backed diction of reality without using formal logic (an invention of consciousness too indeed!), without using any mathematical
language or formalism and without artificial (intuitional!) axioms, what eventually results in a notional construct, imaginable as allegoric
visualisation and describable by usual geometry within the normal three-dimensional space, which we all handle virtuoso after long educational
familiarization and plenty of exercise in daily life, knowing full well however and always keeping in mind that such a 3d-space certainly does
not exist in the targeted 'real world'. ... A whole lifetime searching for methods of maximal abstraction from common sense, this way
ultimately remains the only promising for me to reveal - and subsequently avoid - fixated engrams, when trying to comprehend fundamental physical
laws.
Physicists create models to explain and compile small sections within parts of physical reality which they believe to understand, and they do that
respectively have done in the past very successfully, they are able to compute all values they need, and collectively combine all small sections to
one huge intellectual edifice of many ideas, called physics. All works excellently, and basically there is no urgent need for most of them to
comprehend the building as a whole. Well, some pedants amongst the huge community of builders and architects, in a way the structural engineers,
like to have a closer look on the foundations, to ensure that the building doesn't collapse one day. Unfortunately, they are not as successful as
their colleagues, are still searching for a universal recipe to make one stable footing beneath all these many parts and sections. They aim at a
footing as a profound base plate, preferably independent of all later erected constructions on it, but connecting them mutually and being fully
compatible to all styles of at least those which are proven to stand stable and work reliably.
Meanwhile we wait a too long time for the desired recipe! When I was a young physics student, half a century ago, theories of everything seemed to be
within one's easy reach, enthusiasm was limitless, atmosphere thrilling, but unhappily physical research gradually digressed instead into very
specialized, technical, consumption-oriented and military-related topics, pure foundational research, in epistemological sense, decreased or even
disappeared from academic scenery, at least in my surroundings. Disenchanted, I made my second profession to the first. Today, still waiting for an
illumination, I am deeply convinced, that our 'real world', that reality is totally different from all what we have imagined ever. I tend, as many
others too, to the concept that foundations of reality cannot be reached deductively from physical laws, and that it's best to forget or ignore the
related knowledge and try to entirely supersede the accustomed associations. Concerning this and as promised above, I will name some terms, which I
think they are the most impedimental stumbling blocks on the path to reality.
Anything wrong with this statement: "... all physical objects populate space, and all processes, in which they are involved, take place within space
and time ..." ? It's nonsense! Such sentences arise from 'common sense', which is totally inapt for description of a fundamental physics. The most
important part of common sense is the imagination of space and time, probably rooted in properties and function of the brain, because
everybody has the same or similar associations to words like point, distance, direction, three-dimensional space, volume, flow of time, locomotion
in space, velocity and many others. Such natural associations are self-evident, don't need explanations - but are entirely wrong! At least from the
epistemologist's view, when judging validity of predications or just simple statements concerning reality and our 'real world' on a fundamental
level.
There is no evidence for the existence of a three-dimensional space outside the human imagination! Nor for any other number of
dimensions. Euclidian space, vector spaces and linear independence of their coordinates are inventions of mathematicians and
physicists to explain geometrical and physical laws in a descriptive way, that matches the human consciousness and is congruent with our inviolably
given, ineradicable fixated engrams. Such spaces seem to be logical and simple. Even physicists, despite having learned to abstract, always refer to
it, in all dimensional enhancements, all dynamic geometries, in all topological sophistications - and in quantum field theories as well. Physical
variables there always can be projected someway into the three-dimensional space, which is embedded in the comprehensive system as base or parameter
for alteration of values.
These spaces always imply a continuum for various values, what likewise is not taken for granted - on the contrary: continuum is an
illusionary mathematical construct and not a natural property in the description of the 'real world'. Sure, in quantum mechanics we have Planck
units, but they don't provide discrete values for all other parameters universally.
Another point of discussion is the static of dimensional spaces. Static does not occur in quantum reality! No model of the 'real world'
works sufficiently without underlying dynamic. That's for sure! Unfortunately, mathematics doesn't offer any well-elaborated and consistent theory
of topological systems that are based on respectively 'spanned' by continuously and dynamically changing coordinates, which in turn are inevitable
for dynamic physical entities.
Conclusion: to surmount these first impedimental stumbling blocks we have to forget dimensions and construct instead a space without use of static,
linear and continuous coordinates. It should be possible, and there exist ideas already ...
During last century physicists have developed excellent and comprehensive models of so called 'elementary particles' which work very well and
reliably. Of course, it does not befit me to criticize these images of physical processes and their acting participants, and it is far from my
thoughts to repudiate the findings. The interpretative framework however sometimes evokes my explicit objection. Sentences like "the particle
flies from A to B" make my toes curl. Or even the apparently plain term "particles per cubic kilometre" as measure of density in the universe sounds
totally amiss for me.
Many aspects of particle properties are not sufficiently explained in the theories,e.g. information about punctiform or spatially extended shape of
particles is ambiguous and dependent on experimental and descriptive context, all very factitious seeming interpretations of wave-particle dualism
or quantum physics in general still are completely unsatisfactory, even after thousands of physicists have contributed substantial ideas, starting
hundred years ago, not to mention the attempts to explain the verified nonlocality of particle properties reasonably.
Incidentally, at this point, I cannot refrain from placing some remarks on the megalomaniac plans to replace LHC (Large Hadron Collider, CERN,
Geneva) by the monumental Future Circular Collider (FCC). I used to be a physicist myself and I am highly interested in progress of knowledge, but
this project in my honest opinion is madness, is hubris, is waste of public funds. Invest that money in education and the theoretical
research of thousands of physicists more and you will gain a very much more comprehensive outcome of insights and substantial contributions to a
better understanding of our 'real world'. Readers are invited to inform themselves about the updated background story!
Pure mental contemplation, after having learned the most important absolute facts and having reached an adequate level of abstraction faculty, is
still an important source of cognition, as various mathematical oriented physicists in many ways have demonstrated. Mathematics surely is the only
way to reveal a good part of so far unsolved mysteries and secrets, hidden in reality.
Returning to particles: when we try to see them not as objects that are put into a pre-existing space and manage to treat them as pure
mathematical entities within a space instead, which is not a priori existent but built by just these particles, then we easily approach
solutions without use of the mentioned enormous technic.
The promised mathematical model, I aim to, and which already exists as a 'prototype', explains properties of particles figuratively and
comprehensibly, including quantisation, non-locality, entanglement, interactions, forces, space and time, ...
Many physicists deny the existence of time as an independent dimension for physical processes. So do I. Independent or not, time seems - according
to all experience we have - to be a one-dimensional quantity. Correspondingly we can symbolise time as a line extending from -infinity to
+infinity, infinity premised. If there is a beginning (big bang e.g.) or an end (Armageddon, big rip, big crunch or any other fairy tale), the line
is 'shorter' accordingly, only reaching to (slangy) 'nearly infinity'. I want to demonstrate allegorically that time is redundant and can be
replaced easily by other quantities: when we symbolise space as set of circles with timeline as tangent in point 'now', circumferences being
'distance' to any point in space, we recognize that the symbols for very far located points slowly approximate the timeline and we conclude, that
time is closely connected to infinitely remote parts of space. Perhaps identic to them? Answer will follow ...

fig. 1
From this representation of time follows the next thought: big bang - if we posit that it has happened - was not the beginning of time but the end of
an until then infinitely long-lasting time, respectively the abrupt transformation of an infinite, perhaps one-dimensional, quantity into an
infinite pattern which immediately undertook all functions of 'eternal time', making time absolutely redundant. That way we avoid the
epistemological problem 'creatio ex nihilo'. Any infinity was pre-existent and appearance of space and matter wasn't a creation but 'only' a
transition from one state of infinity into another, from smooth, steady, linear and continuous conditions into distinguishable discrete parts with
the capability of mutual interactions between all the newly emerged components.
To illustrate such a transition, we maintain the pictorial representation of time above. The circles shall be tightly packed, with no spacing between
neighboured circles. Then the complete set of circles is equivalent to the infinite timeline (mathematicians, familiar with set and number theory,
hopefully will approve), and an imaginable transformation could be a turn of the timeline around itself. The turn of a one-dimensional line cannot
be recognized, but when we replace the line by the set of circles, we get, by the rotation, a new set of nested horn tori, all interlaced into one
another with identic centre, simultaneously the boundary point, named 'now', on tangent timeline. Time - as an independent dimension - has vanished
silently, while 'space' and 'matter' had emerged explosively. And today, we humans, late result of that transformation, reduce our creator to a
simplifying auxiliary physical term and to pure human psychological perception.
To find more details about the character of time and subsequently of other physical terms, explained allegorically by horn tori, we have to go far
afield and delve deeply into the matter. But first, another related thought: the simplified image of a spontaneous transformation from a
one-dimensional infinity to an infinite discrete pattern as indicated above, implies that this process didn't take place at one single point as
origin of further developments, but it happened all over the linear infinity simultaneously. The decay into discrete constituents, sudden loss of a
pre-existing continuum and drastic depletion of spatial points simulates an inflationary scenario in the new space. As effective mechanism for the
whole process we again adduce these horn tori, but their static geometry now endued with a particular dynamic, always keeping in mind however, that
horn tori only are symbols and equivalent representatives of complex manifolds.
Basics of horn torus geometry, topology and dynamic are described in detail on this website [1] with many
explaining illustrations in links.
To follow interpretations of horn torus properties as physical phenomena, it is inevitable to familiarize first with the model, the provided
analogous images and the geometrically representable dynamic. One at first has to be able to relate to revolution, rotation and mutual unrolling of
interlaced horn tori, nested into one another, and to the mechanism of generating trajectories or cycloid lines on their surface. Then many obscure
physical terms, concepts and phenomena appear no longer mysterious and unexplained, but become logical, clear and evident.
Here I only want to list a couple of terms and the related representation by horn torus properties, time at first again: timeline is the main
symmetry axis on which the nested set of horn tori moves (unrolls) in one direction. Motion in opposite direction corresponds reversion of
time, leading into the world of antimatter. Unrolling is closely related to poloidal torsion of the horn torus bulge, what we call
'revolution', while 'rotation' is used for the toroidal spin around timeline.
Combination of both turns leads to the mentioned trajectories, for certain ratios of angular velocities as Lissajous figures ('resonances'),
identifiable as particles. Geometric situation and dynamic are absolutely independent of size (scale) and angular velocity of turns. The
system of nested horn tori shows a perfect self-similarity, what generates a universally valid unit (ratio 1:1) and thereby a self-metrisation of
the space that is defined by the dynamic set of horn tori. As first properties we detect the constancy and the maximum value of revolution, easily
identifiable as speed of light c. Mentioned ratio 1:1 will turn out to be related to Planck units: one revolution of the
unit horn torus corresponds to Planck length ℓP, one rotation accordingly to reduced Planck constant ħ,
Planck time tP remains redundant.
With the horn torus model we intend to suggest alternate associations to space, time and physical objects on a very fundamental level, where only
'entities' exist and not complex compound things yet. The analogue model does not target macro-physical properties at all - it is not suitable to
describe or explain them. Forces however, despite quantifiable just in macro-physics, have their origin in particles and space, why they are crucial
subject of attention here too.
To define forces, we have to find and describe the cause for locomotion of particles or physical objects within the space they 'populate',
independent how space is defined. All fundamental forces (gravity, electromagnetism, strong and weak force) are manifestations of any mysterious
'interaction' between particles resp. physical objects. Physicists are able to describe them mathematically, calculate exact values, and make
accurate predictions, but the deep principle or mechanism behind that interactions still is completely unknown - and vector spaces, I am deeply
convinced, never will lead to the final answer.
In the horn torus model, space is spanned by non-linear, dynamically changing coordinates [2], called 'entities', and each entity contains a complete cascade of all different particles. The coordinates are not linearly
independent, but act as physical objects themselves by interaction with all other coordinates or entities. They are represented in every spatial
point each, as section of the coordinate in the form of a particular horn torus with specific size and ratio of turns.
A horn torus, unrolling along the trajectories of other horn tori which are located in the same spatial point, is forced to change its rotation speed
due to avoidance of - figuratively! - 'slippage', and therefore also changes its size, because within the same entity a firm correlation exists
between size and rotation speed of every horn torus. At a certain distance from the 'origin' (size zero) or also from the unit horn torus, there is
always only one single definite ratio of the angular velocities, revolution to rotation, and only one size, inversely proportional to the revolution
angular velocity [3]. The entire entity - together with its origin and with all associated
particles - then shifts to new positions related to other entities without changing its internal structure, and that means the particles move closer
or move away from other particles, depending on the change in the rotational speed.
The cause for locomotion of particles - in other words: force between particles - is now reduced to one single mechanism. Only the name for this
unified force is different in distinct portions of an entity: gravity acts at the sections of large horn tori, up to infinite size, the other
forces at sections between sizes, defined by their ratio of angular velocities, electromagnetic interaction between 1:2 and 2:1, strong interaction
between 2:1 and 3:1 and weak between 3:1 and 4:1 ... [4]
With the analogue horn torus model, we leave 'classical mathematics'. Though we pragmatically make use of well-established skills in three dimensions
to illustrate the dynamic, the model is not dimensional - neither Euclidean nor non-Euclidean, neither related to any vector space nor even
connected to Hilbert spaces and the respective formalism - at least not in an obviously predominant way. Horn tori induce an extremely
dynamic and complex geometry and simultaneously are capable to form a nearly static 'flat space' with Euclidean rules when approaching
'infinite size'. Conventional methods are insufficient or too labourious to describe such a hybrid of dynamic and static space properly, and we
maybe have to await further progress in quantum computing for an appropriate approach and adequate treatment, and for a - maybe disruptive -
congruent mathematical model of physical 'reality' that comprises the pervasive and unstoppable dynamic as main intrinsic property.
Anyway, the known and widely accepted classical mathematics fails yet to reveal the secrets of physical reality, probably because our mathematics is
incomplete still, doesn't provide the dynamic code that rules our world, and on the same time it contains a lot of ballast that is adverse to
physical interpretation. A physically relevant complete mathematics has to comprise this mentioned unique code and has to be self-consistent,
without contradictions.
To obtain such a mathematics, the classical formalism has to be extended significantly, but for self-consistency simultaneously knocked into proper
shape in many respects. Physical laws have to be 'true' and 'real' and a priori valid, not invented by men but discovered, while mathematical rules
often don't comply with these conditions in a good consistent way. Too many axioms have been established intuitionally during the long
history of mathematics. Physical reality is not based on axioms and also does exist in absence of human consciousness, then admittedly without all
the properties we perceive, associate and attribute to 'nature'. Physical reality, even when not observed, at least exists as a kind of
mathematically representable pattern. These patterns and/or 'structures' don't contain the familiar 'self-evident' constructs of our perception and
imagination, but are inevitable synergetic effect of fundamental entities, which exist from the 'earliest beginning' of our universe and which
interact with one another in a simple, deterministic, fantastically intertwining manner ...
To describe this interaction of fundamental entities mathematically, will be a later aim. At first, we have to get hold of one single entity, above
also called coordinate, and we have to identify its constituents, the 'particles'. When we are able to describe one of them entirely, we know all
the others, and if we manage to describe the entity as a whole, its interactions inclusive, we know the universe.
In my interpretation, the term 'mathematical universe' should not be applied to the physical phenomena, which we realize, perceive and interpret in
'nature', and for most of them we already have excellent mathematically formulated laws. A mathematical universe concept has to be a basic
physical theory concerning 'creation' of space (beginning, e.g. big bang) and cosmological topics (inflation, expansion, further evolution of
primordial constituents to 'elementary particles', 'energy', matter, atoms, molecules, galaxies, ...) exclusively by pure abstract
mathematics. As main premise for full abstraction we imperatively need strict epistemological reductions and fundamental definitions of space, time
and physical objects as entities. Neither terms from outside mathematics nor traditional imaginations of objects and processes are allowed in the
applied formalism.
One of such concepts, admittedly in the state of a preliminary intellectual game, is the above often mentioned horn torus model. Horn tori are pure
associative symbols for complex numbers. All what we explain by horn tori, is an utterance concerning properties of complex numbers. We even reduce
to integral numbers, (1,1) being a natural unit for metrisation. It is the pair with smallest possible absolute value within the model, because
(1/n,1) in the interpretation 1/n rotation per 1 full revolution is the same as 1 full rotation per n revolutions. (1,1) remains the smallest
reference for all other ratios, and there are no fractions of revolution and rotation - only integers. With this so called 'standard dynamic horn
torus' we possess a natural source and simple explanation of quantization!
Metrisation of the horn torus space and an easy explanation for constancy of light speed arise from the perfect self-similarity of nested horn tori,
all being part of fundamental entities, but to reproduce that imagination, faculty of abstraction is challenged maximally and readiness for broad
familiarization is indispensable. Trials of assistance are provided on many pages within this website.
The relatively simple basic image already produces lots of properties within the model and accordingly in the hereby emulated universe. Higher
complexity of any level can be reached by iterated substitutions of real parts of the complex numbers by new complex ones, then ultimately leading
to - already known - extensions of the number system, to quaternions, octonions, sedenions. ... Anyway, the most promising, presumably the
only, method to understand our universe roughly, is a mathematical one. Until now, empiricism alone hasn't brought fundamental insights, despite
alleged successes by colliders and suchlike. Nature hides its secrets:
All our many models of the 'real world' are crutches only, to hobble around the never reachable and imaginable truth, solely to enjoy the short,
rare moments of supposed close encounter with it - but it's worth to undertake and experience that!
In the following we want to go a bit further into the model, but to emphasize it again: the horn torus model is neither a mathematical nor a physical theory,
it is not science at all, it is rather a symbolic, analogical representation, using allegoric visualisations of fundamental physical entities, playfully
aiming for different interpretations of fundamental processes, for an exciting creation of novel insights and for an amazing enhancement of existing
explanations. Don’t expect a stringent and structured scientific treatise, but note instead, that all statements remain on an ontological, epistemological,
philosophical level. *
The horn torus model is an attempt and a proposal to describe foundations of our 'real world' in an assumed manifestation as unconscious universe with
no properties others than mathematical. Constituents aren't space, time and matter, but only numbers in their simplest form: natural numbers, as complex
integers first, later - as required - easily extendable to quaternions, octonions, sedenions, again with integer parts each. Nested horn tori, dynamically
interlaced into one another, illustrate as eidetic geometric analogue, that numbers quasi are able to interact with one another and - e.g. by mutual
'annihilation' - to transform their initial continuum into discrete structures by a simple pattern generating process, leading to intricate results,
which are interpretable as entities or 'coordinates' of a dynamic but timeless space with striking analogies to our 'real world’.
We indeed possess mathematical descriptions for all realized physical processes and apply them very successfully, without any doubt, but no actual accepted
model of nature describes all in one big idea, no one comprises all aspects of experienceable ‘reality’, and furthermore - most important - there is a lack
of appropriate images which illustrate objects and processes in such a way that they match the human thought structure and mental capability
adequately.
Here starts the relevance of horn tori. The associated model tries to fill the lack of imagery, what most of us need for a good understanding. Dynamization
of horn tori, illustrated in an easily intelligible pictorial way, generates multifarious and sophisticated new properties, and there will open a
completely new mathematical world which bears the possibility to see and describe the fundaments of our ‘real world’ in a quite different and potentially
most comprehensive way. Dynamic of space is the magic word. Not in the sense of geometrodynamic, where our familiar three- or more-dimensional
space somehow is distorted dynamically. The space, we head for with the horn tori, is not spanned by dimensions, it is neither a Euclidean nor non-Euclidean
space, nor any vector space, not even in the sense of the abstract Hilbert space - it is spanned instead by continuously and dynamically changing
coordinates.
We dynamize the primarily static figure horn torus - I repeat that again and again, to emphasise the underlying principle - by introducing rotation around
the main symmetry axis and revolution of the torus bulge around itself, detect the then emerging trajectories on the surface, observe their paths, which
depend on the ratio of turns, let the horn torus change its size according to the ‘unrolled distance’ by the revolution, what again changes the mentioned
ratio and the trajectories, then interlace different horn tori by nesting them into one another with common centre, interpret the superposition or mutual
interference of trajectories as particle interaction, finally abstract from the three-dimensional space of imagination to the effect that we renunciate
dimensions at all, which in common view span a physical space as container for physical objects, and - as quintessence of all previous mental efforts -
detect that our new space is ‘dimensionless’.
That all sounds extremely intricate and artificial, and to realise, that the three-dimensional space (likewise all linear vector spaces!) shall be a man-made
construct and not an a priori existing entity, seems to be difficult to place within the scientific community. But an open-minded unbiased readiness for
broad familiarization with the allegoric images and processes, leading to a far-reaching abstraction from most traditional ideas, soon enables you to revel
in new interpretations, perceptions, cognitions, and lots of aha experiences.
The dynamic horn torus model highlights and perhaps reveals big mysteries in our comprehension of ‘reality’, at least in an allegorical, descriptive sense
for issues concerning intrinsicality of time, space and physical objects, continuum vs. discrete nature of space, metrisation of space, origin and cause
for quantization, minimum values, constancy and maximum value of lightspeed, non-locality of quantum processes, entanglement, arrow of time, determinism,
causality, ...
In our intellectual game we reduce the many (too many!) necessary components of the standard model to one single principle, which underlies all physical
objects and processes as a unified mathematical structure or rule, by introducing graphically describable and imaginable all-embracing fundamental entities.
But again: I want to emphasize, that the horn torus model is neither physics nor mathematics, and least of all it is esotericism or anything like ‘holy’ or
‘sacred’ geometry! It is a pure intellectual game to realize generally, that fundamental entities as representation of physical objects, processes,
elementary particles, and space are imaginable and constructable.
Origin of the idea (in 1988) was the endeavour to find an analogously figurative visualisation of complex numbers, different from the well-known static
Riemann sphere. Target was to illustrate dynamic physical processes which very often are described mathematically by means of complex numbers - be
it in electrodynamics, relativity or in quantum mechanics. As proposal then emerged that the real part shall be represented by the rotation of a horn torus
around the main symmetry axis, the imaginary part by the revolution of the torus bulge around itself, measured in degrees of rotation respectively
revolution, not as localisation on the horn torus surface. The dynamic figure replaces the Riemann sphere, and values of complex numbers thus are
represented and visualised dynamically.*
Main principle of the dynamic horn torus is that it rolls along an imaginary axis i·t with constant ‘speed’ c and changes its size
according to the unrolled ‘distance’ on this axis. Without rotation around the axis, the difference of horn torus longitudes before and after a motion
corresponds to the unrolled distance during ‘locomotion’, shown in link [3]. Circumferential
speed is constant, but angular velocity of revolution depends on size: these latter quantities are inversely proportional. When we now add rotation, the
situation gets more intricate: the place of the unrolling longitudes undertakes a trajectory, which figuratively unrolls without ‘slippage’ on the axis.
These trajectories, ‘unrolling lines’ or cycloids show a particular pattern on the horn torus surface, according to the ratio of revolution and rotation,
more precisely, to the ratio of their angular velocities. Here, in fig. 2, we show some trajectories for different ratios in a perspective view:
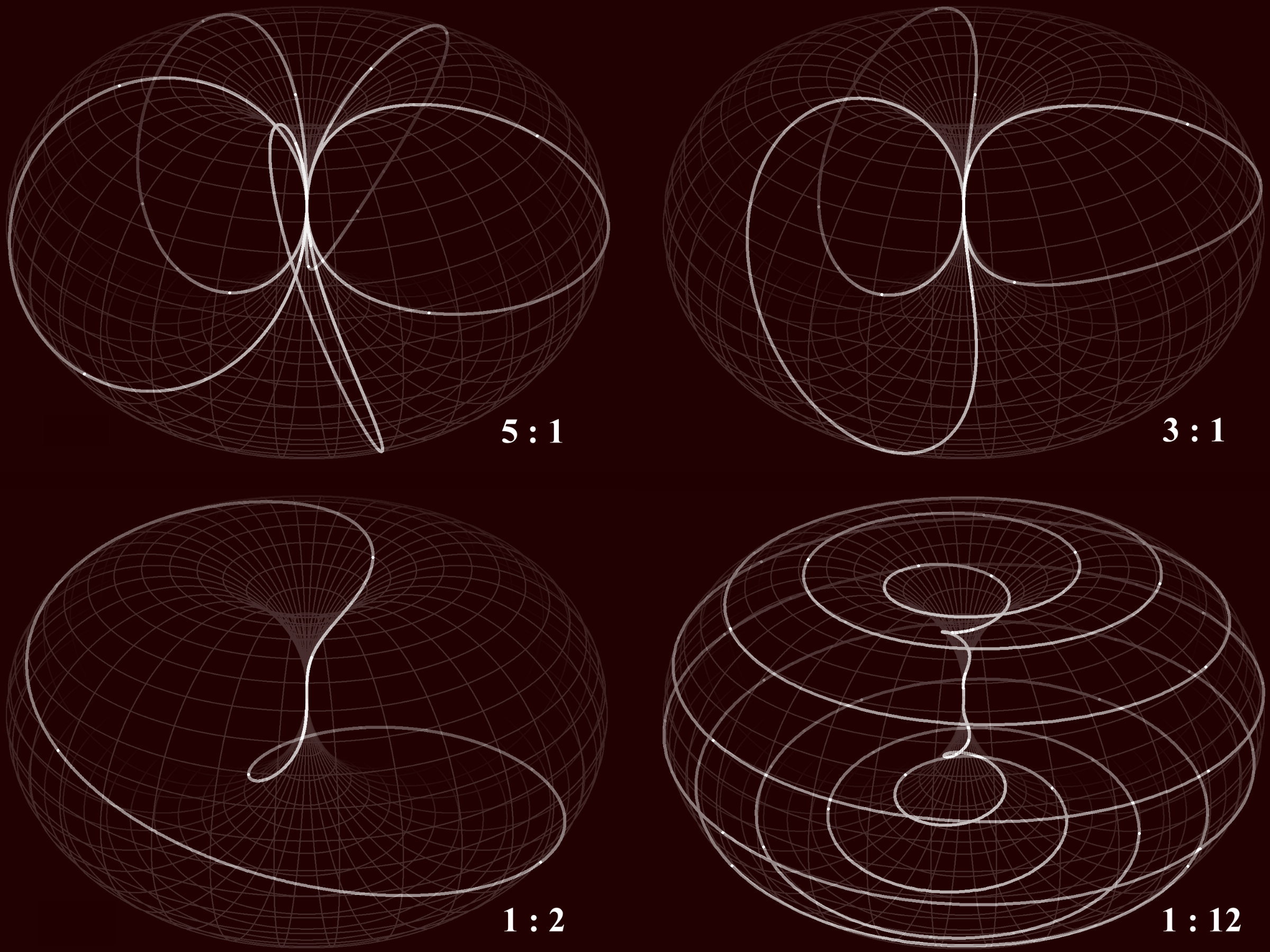
fig. 2
The examples in fig. 2 show trajectories for rational ratios (revolution : rotation). For ratios ≥ 1 they loop (repeat) after one rotation, for ratios ≤ 1
after one revolution. I call them resonances or Lissajous figures on horn torus surfaces. During unrolling along the axis, a horn torus
changes its size and therefore passes all possible ratios and all resonances as well. For small horn tori we see many revolutions per rotation and for
big horn tori many rotations per revolution. A kind of mathematical mirror is the ratio 1:1, and in the physical interpretations it will appear to have a
very special meaning. The related figurative object (fig. 3) is called ‘standard dynamic horn torus’.
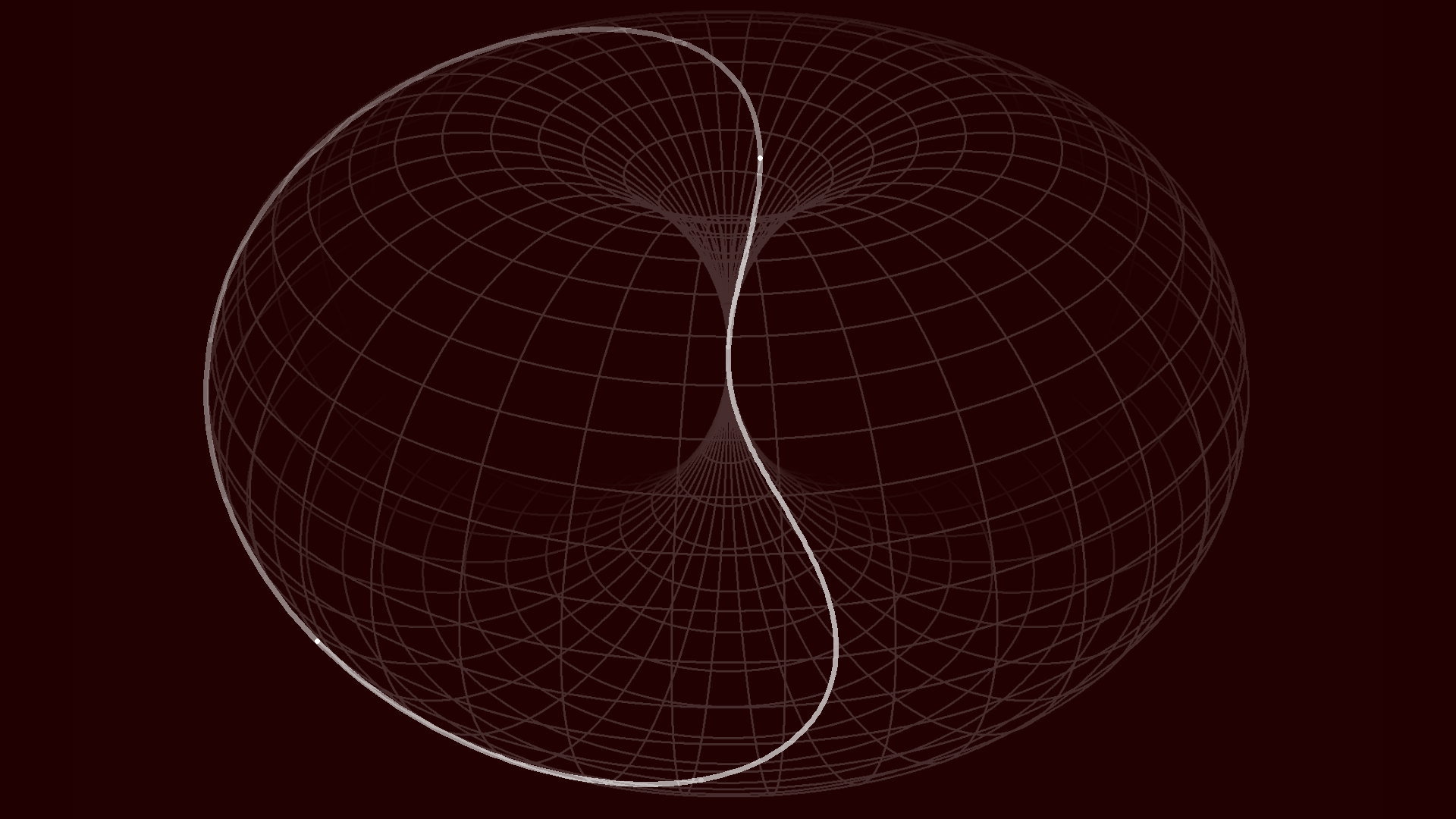
fig. 3
To anticipate later considerations: the standard dynamic horn torus already symbolises some of the most fundamental quantities. For this unit
horn torus, we determine that one revolution represents Planck time tP and the circumference of a longitude (meridian) Planck
length lP (in a different interpretation: length of the 1:1-trajectory), while the circumferential speed of revolution is light speed
c, and one rotation represents Planck’s reduced constant ħ.
The unit horn torus divides the set of all (infinitely many) possible horn tori into two parts. Those with ratio revolution : rotation > 1 have a smaller
(down to infinitesimal) size, compared with this unit, and we see trajectories with more than one loop around the torus bulge per one rotation, while
tori with ratio < 1 are bigger (up to infinitely large) with more than one ‘spiral’ around the rotational axis per one revolution of the bulge (compare
examples in fig. 2).
The complete set comprises all horn tori, all sizes, and all ratios (but note, size and ratio are not independent, they are inversely proportional!), and
we designate it as ‘fundamental entity’. A particular horn torus occurs exactly once in the set.
To give an impression of the complexity, we now draw a simplified graph of this entity, represented by the ‘unrolling line’ in dependence of an
increasing r, selected between ratios v(φ) : v(ω) = 10 : 1 and v(φ) : v(ω) = 1 : 1000, but not to scale and using rather rough
differentials dr for the single steps (otherwise the lines would lay very densely). r is horn torus radius, v angular velocity, φ revolution, ω
rotation. See again animation in link [2].

fig. 4
The related parametric form must be established for both parts of the entity separately in the following way (setting r = 1 for ratio
v(φ) : v(ω) = 1 : 1)
For case r > 1, r and ω increase with φ, starting with φ1 = 2π,
and according to r = φ / 2π (↝ r1 = 1), ω = r·φ = φ2 / 2π (↝ ω1 = 2π),
we have
x = (1 – cos(φ))·cos(φ2 / 2π)·φ/2π
y = (1 – cos(φ))· sin(φ2 / 2π)·φ/2π
z = sin(φ) · φ/2π
For case r < 1, 1/r and φ increase with ω, starting with ω1 = 2π,
and according to 1/r = ω / 2π (↝ r1 = 1), φ = ω / r = ω2 / 2π (↝ φ1 = 2π),
we have
x = (1 − cos(ω2 / 2π))·cos(ω)·2π/ω
y = (1 − cos(ω2 / 2π))· sin(ω)·2π/ω
z = sin(ω2 / 2π)· 2π/ω
The parametric forms show mirrored conditions, so, as already mentioned, the unit standard dynamic horn torus indeed is a kind of mirror within the new
mathematical world, and likewise, as physical interpretation, it separates the big ‘outer’ world, consisting of electrons and photons from the small
‘inner’ atomic and nuclear realm.
Next step should be, that we interlace entities into one another, maintaining a common point for all, namely the point S (S for symmetry or singularity),
the centre of all nested horn tori. But alone the complexity of one single entity indicates that this endeavour appears to have no prospect of success,
when we apply common mathematics only. But it could be worse. For our aim, to get an idea of the model, it is enough to understand the principle of
nesting two or a few horn tori into one another. As first impression here two (fig. 5, animated in link [5]) and twelve (fig. 6) nested horn tori:
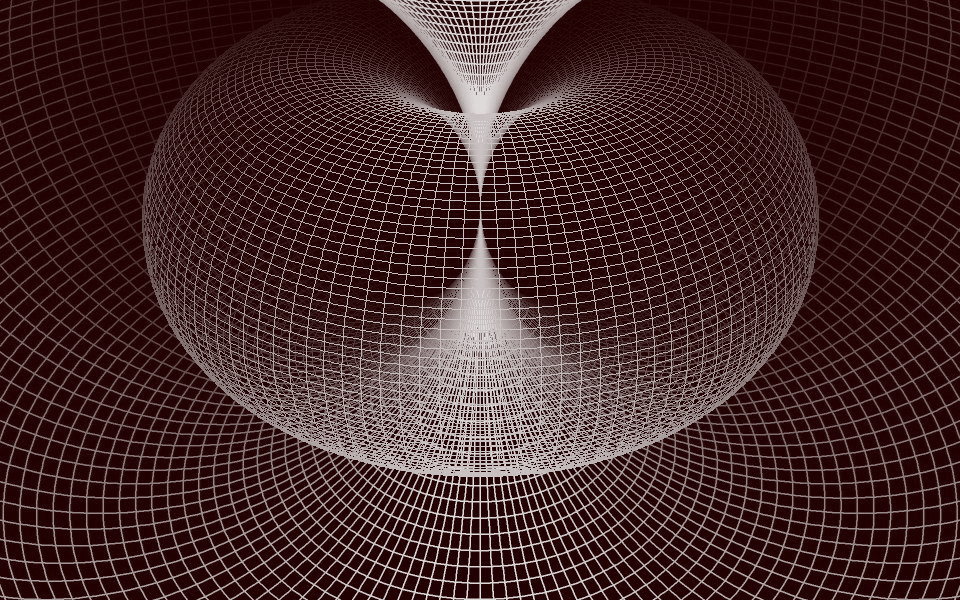
fig. 5
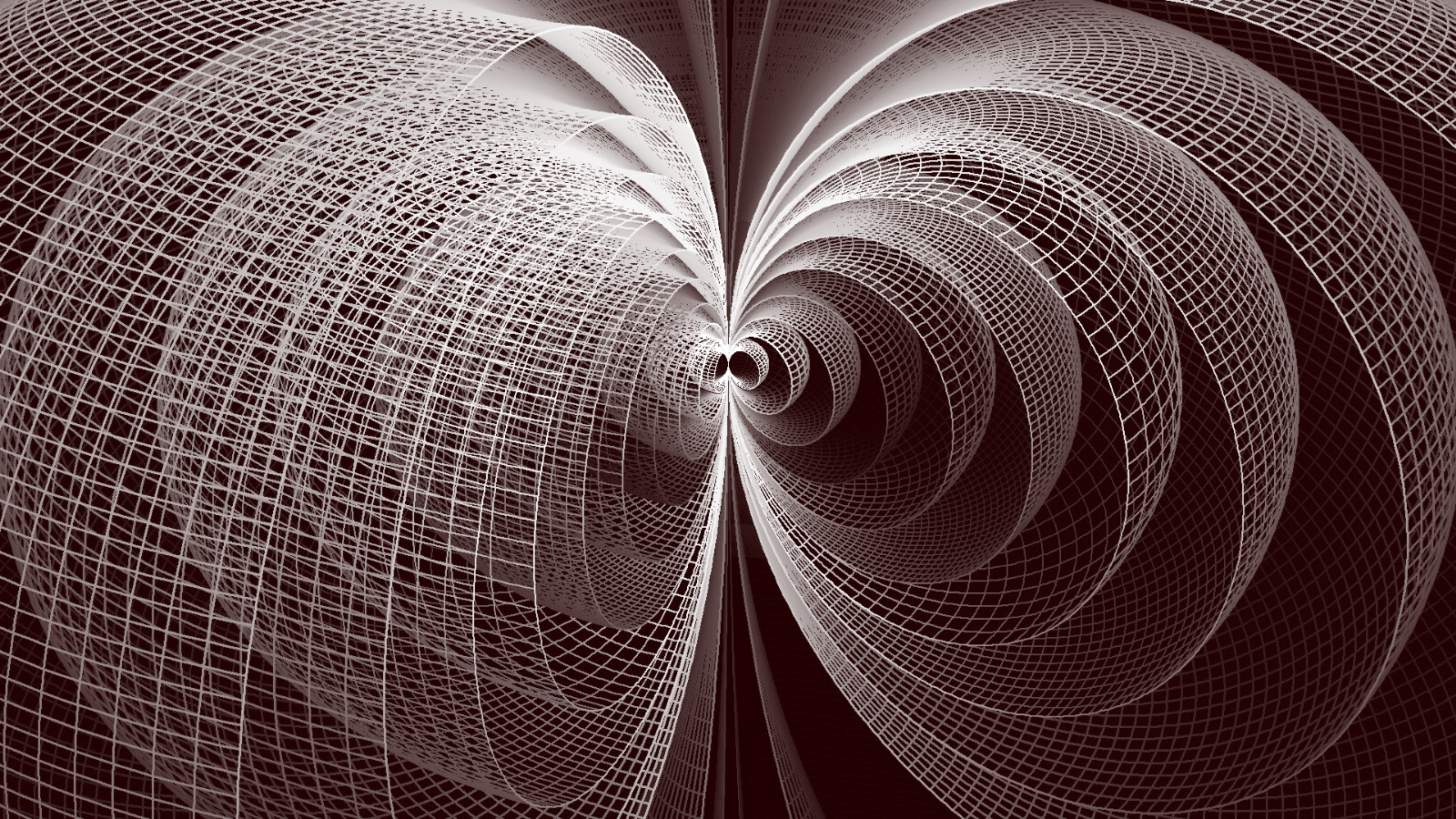
fig. 6
(a 65° wedge is removed to highlight the nesting)
The dynamic, however, as most important intrinsic property of the model, cannot be described properly and comprehensively by static depictions like the
above ones. We need moving pictures, animations, simulations for an adequate presentation of dynamic. In this printed publication we have no choice but
to provide links to respective webpages, where such animations can be viewed.
The linked animation [2] shows a wide section of a single entity in a coarse, simplified
depiction of the dynamically uncoiling horn torus coordinate. The ‘unrolling line’ starts parallel to longitudes on a very small horn torus, forms
Lissajous figures, when passing rational ratios revolution : rotation, which are shown as ‘resonances’ with short stops during increase of size, and
approaches infinite size with parallels to latitudes, without resonances. The animation possibly might lead to the following:
Physical interpretation
Sharp resonances represent fermions, the sections between them bosons, and the lines without any resonances on big horn tori (ratio << 1) are photons.
In this way all kinds of elementary particles are beaded on one thread, within one single coordinate, forming a unique ‘fundamental entity’. What appears
to be a ‘particle’ is only the ‘local’ property of the much more comprehensive entity at a specific ‘location’ in the horn torus space. What we describe
as a nucleon here, is an electron there, farther away a photon, and simultaneously a completely different ‘particle’ of the same entity elsewhere.
Now we combine another or more entities with a singled-out entity by nesting them in their common point S. Place of ‘interaction’, where a horn torus
unrolls on a trajectory, always remains this centre. It is the ‘spatial point’, to which any ‘particle’ in the universe is connected as one portion of
its individual ‘entity’. All infinite many ‘particles’ of the universe are represented in every ‘spatial point’. Every horn torus shares the common
tangent with all other horn tori, when they are nested into one another at their centres. Size of a horn torus symbolises the ‘distance’ to the location,
where the associated entity (the dynamic coordinate) converges to size zero. Different ‘spatial points’ differ in the combination of horn torus sizes.
All combinations with natural numbers (explication for that see links below) of sizes are possible, forming an infinite-dimensional regular pattern.
All paths through this discrete pattern (space) are equally possible, and every horn torus can unroll at a trajectory formed by any
other horn torus as interaction at any ‘spatial point’.
This space is by its definition a multiverse (due to infinite many paths) with non-local correlations between ‘particles’. A limited neighbourhood
of every ‘spatial point’ contains the complete information about one selected universe. With this property one - by the way - immediately recognizes the
possibility that big bang has not started out of one tiny spot but rather took place all-over a pre-existing just one-dimensional infinity. Much more
information you will find on linked websites.
* Remarks
• In conventional, familiar mathematics and physics, the static horn torus serves as an extension of the well-known Riemann sphere. The existing
bijective conformal mapping between both (discovered by me 2018 [6],[7]) distinguishes the horn torus as a member of complex manifolds. So, wherever you apply the
Riemann sphere in theoretical physics, you may replace it by the equivalent horn torus and instantaneously gain a lot more properties of the described
object!
• In retrospect, with a view onto history of science, horn tori could be associated with the ‘ur-alternatives’ by C.F.v. Weizsäcker, but also with
spinors, Penrose’s twistors, Lie groups and all related - also current - symmetry considerations.
• The (allegoric or analogously figurative) dynamic horn torus model primarily only provides ontologically relevant interpretations. These can be used to
justify and substantiate a philosophical worldview that can be assigned to subjective idealism or constructivism, and on the basis of which both axiomatic
mathematics and phenomenological physics are regarded as not real (independent of consciousness). As first conclusions, among others, one perhaps
could state these:
- There is no empty space in which physics takes place. Complex dynamic processes generate the space, an idle state (statics) does
not occur.
- There are no ‘dimensions’, neither a Euclidean nor non-Euclidean space, nor any vector spaces, not even in the sense of the abstract
Hilbert space.
- Time is not a basic physical quantity, it is included and identifiable in the model, but is redundant and reducible to more fundamental
quantities.
- Without a consciousness that describes them, there are no individual, independent ‘physical objects’, especially no isolated or
isolatable particles.
- All entities, i.e., all ‘particles’ too, are connected (linked, entangled) with all other entities or ‘particles’ of the
universe and ‘interact’ with each other.
- Interacting means being dynamically interlaced, constantly measuring and comparing each other and deterministically integrating into an
entirety.
- The universe is an orderly, mathematically describable network, a regularly structured pattern, the mere structure of an a priori existing
mathematics [8].
- A consciousness uses its special senses to pick out only very small parts of this abstract mathematical pattern from the comprehensive total
of processes.
- All described properties of what is perceived are interpretations by the perceiver, generated by subjective mental processing.
• After science for centuries ignored the existence of the geometric figure horn torus completely or neglected its relevance unduly - nearly nobody
realized, described and applied the exceptional topology, maximum symmetry, high complexity and creative capabilities of this unique object - it now, in
recent years, increasingly appears in publications, mostly in context of particle and quantum physics and in connection to cosmological questions. The
subject is developing and promises to stay exciting for a good while.
• Postulation as a consistent theory, based on the horn torus model, will be an ambitious project for physicists in the future, after mathematicians
and computer programmers will have established methods to handle that dynamic. I'm afraid we need a different, perhaps disruptive, ‘fundamental’
mathematics.
• An introductive explanatory video (16 min.) is provided in link [9], also uploaded to
YouTube, amongst some entertaining, horn torus related videos.
P.S.: Meanwhile I have deleted my channel and all contents on YouTube, but look here:
https://www.artmetic.de/graphics/video/horn-torus-videos.html
References
This is not a scientific publication and there are no external references provided,
all texts and illustrations originate from author’s private websites (2000...2023):
[1] https://www.horntorus.com/ (provides all information)
[2] https://www.horntorus.com/illustration/URLdetail.html
[3] https://www.horntorus.com/illustration/increase.html
[4] https://www.horntorus.com/text/16_unification.html#txt
[5] https://www.horntorus.com/illustration/2nestedhorntori.html
[6] https://www.horntorus.com/manifolds/conformal-mapping.pdf
[7] https://www.dorntorus.de/d (original texts in German, 2000)
[8] https://www.mathematical-universe.com/ (short synopsis)
[9] https://www.bighiss.video/ (related explanatory video)
The author, Wolfgang W. Däumler, used to be a (theoretical) physicist and a
physician (anaesthesia, emergency medicine and critical care), was/is active in
several more fields (aviation, navigation, architecture, programming, digital art, …),
now retired and lives in Allgäu, South Germany.
W.Daeumler
CV
memoirs
↑ top ↑ sources (© W.Däumler):
Horn Torus & Physics
sitemap
frontispiece 1 ·
2
fig. 1 ·
2 ·
3 ·
4 ·
5 ·
6