conformal mapping from (Riemann) sphere to horn torus surface
 
 endeavour:
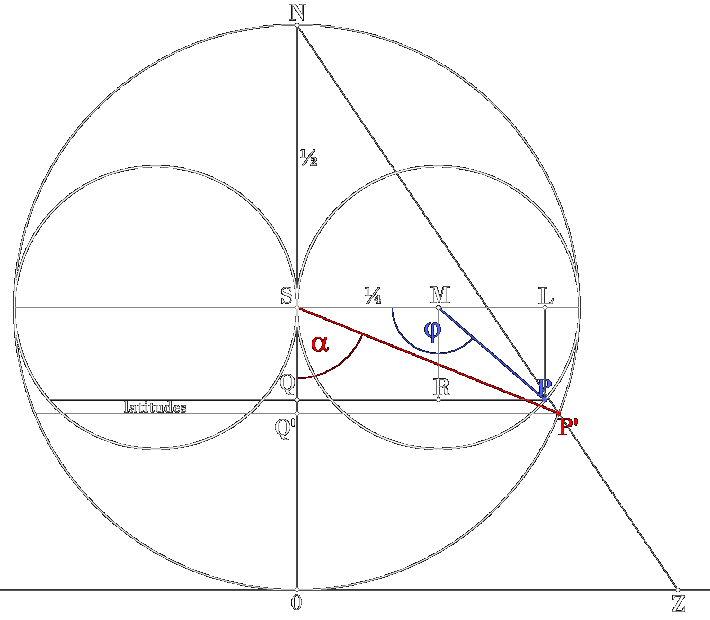
transfer point P' on sphere to a point P on torus, equivalent angle α → angle φ  (see sketch),
without changing shape and angles of projected or mapped figures, e.g. circles
 
 denotation of points:
(all points lie on the same plane that contains the main symmetry axis of the horn torus)
P' : any point on (any!) sphere, here we particularly cover the Riemann sphere
P : mapped point on nested horn torus, but compilation will also be valid for any horn torus!
Z : position of related complex number (x,y) on complex plane in case of Riemann sphere mapping
0 : center of complex plane (Z = (0,0)) and south pole of Riemann sphere (plane is tangent to sphere)
N : north pole of sphere, origin of Riemannian stereographic projection Z ↔ P'
S : common center of sphere and horn torus (not the south pole of sphere, notabene! I insist
  on this denotation for the horn torus, because S stands for for Symmetry and Singularity!)
M : center of torus bulge cross-section circle
Q : intersection of perpendicular from point P on line ON
Q' : intersection of perpendicular from point P' on line ON
L : auxiliary point on line through S and M, intersection of perpendicular from P
R : auxiliary point on line QP, intersection of perpendicular from M
 
 angles:
α = ∠0SP'  (0 < α < π, α = 0 for P' = point 0, α = π for P' = N)
φ = ∠SMP  (0 < φ < 2π, φ = 0 for P = S  and/or  φ = 2π for P = S)
ω : rotation angle around symmetry axis (0N) = position of longitude (meridian) on sphere resp. torus
 
 procedure:
we don't declare any appropriate stereographic projection to proof afterwards the conformality but
use instead the conditions of conformality to compile and establish the wanted mapping analytically:
for this we construct small circles on the surfaces of sphere resp. horn torus around points P' resp. P
by equalling their radii that lie on longitudes and on latitudes of sphere and of horn torus respectively.
in the sketch the longitudes are the cross-section circles on wich points P' and P are positioned and
the latitudes are circles perpendicular to the drawing plane through P' and P with radius Q'P' resp. QP,
they lie, half each, in front and behind the drawing plane, Q' and Q being centers of the latitude circles
 
 compilation:
for Riemann sphere is valid: length of longitude (meridian) m = 2π·r = 2π·½ = π
and length of latitude l = 2π·Q'P' = 2π·½·sinα = π·sinα
for horn torus we have as length of longitude m = 2π·¼ = π/2, the latitude is slightly trickier:
its radius is QP = QR + RP = SM + ML = ¼·(1 + cos(π - φ)), so latitude l = 2π·QP = ½·π·(1 - cosφ)
now we consider infinitesimal circles around P' and P on the surfaces of sphere resp. horn torus
and equal their radii dm on longitude and dl on latitude, noting that dω is identic for both figures
on sphere is dm = ½·dα, dl = ½·sinα·dω, and so for dm = dl we get  dω = dα / sinα
on horn torus is dm = ¼·dφ, dl = ¼·(1 - cosφ)·dω, for dm = dl we get  dω = dφ / (1 - cosφ)
finally we have to integrate a relative simple differential equation:  dα / sinα = dφ / (1 - cosφ)

Riemann sphere:  0N = 1 ,  ∠0NP' = α/2 ,  ∠0ZN = π/2 - α/2 ,  |z| = 0Z
  gif
 
note: the solution is valid for any sphere and any horn torus !  ( → as  pdf )
see : numerical computation and check for conformality (Excel-files .xlsx)